ボクにもわかる地上デジタル - 地デジ基礎編 - 電波伝搬

　　　　　　　　　　　　　　(作成:2004年04月)　　　　　　地デジTopへ戻る
　　　　　　　　　　　　　　(更新:2006年05月)

自由空間損失

　　　ある点（送信点）から電波が全ての方向に放射されたとします。（実際の
　　電波を点から全方向に放射することは難しいのですが、ここではそのように
　　仮定します。
　　　送信点で与えられた電力は電波となって全方向に広がってゆくので、徐々
　　に電力が薄まってゆきます。薄まり具合は、球の表面積に反比例します。
　　　ここで距離rの位置での電波の強さを考えてください。全ての方向に距離r
　　ということは、送信点から半径rの球に広がってゆくことになるのです。
　　　球の表面積の公式は4πr^2です。つまり、電波は距離rに対して4πr^2ずつ
　　薄まってゆき、この薄まり具合を「損失」と呼びます。
　　　また、障害物が無い場合の損失を「自由空間損失」と呼んでいます。

　　　　　　　　損失LOS　 ＝ 4πr^2 / Ae
　　　　　　　　　　　　　　　　　　 ￣￣　　　　　アンテナ開口面積
　　　　　　　　　　　　　　　　　　　　　　　　　　Ae=(λ^2)Ga/4π

　　　　　　　　　　　　　＝ （4πr／λ）^2　…………フリスの公式
　　　　　　　　　　　　　　　
　　　さらに、デシベルに変換すると、次のようになります。

　　　　　　　損失LOS[dB] ＝　20 * log (4πr／λ)　……自由空間損失

　　　　　　　　　　　　　　　　　　　　　　　　r : 距離
　　　　　　　　　　　　　　　　　　　　　　　　λ: 波長(=光速c/周波数f)

　　　　　　　　　　　　　　　　　　　　　　　　LOS=Line of Sight

　　　
大地反射波

　　　前節では球面状に広がってゆく電波について、自由空間損失を考えました。
　　しかし、現実には様々な物体などにぶつかりながら電波は伝搬します。
　　　地上波放送の電波伝搬で最も大きな障害物は「大地」です。大地での反射
　　波による損失は下式で得られます。

　　　　　　　損失REF[dB] ＝　20*log ( abs( 2*sin( 2π*h1*h2／(ｒλ)) ) )

　　　　　　　　　　　　　　　　　　　　　　　　h1: 放送局の高さ
　　　　　　　　　　　　　　　　　　　　　　　　h2: 受信アンテナの高さ
　　　　　　　　　　　　　　　　　　　　　　　　λ: 波長(=光速c/周波数f)

　　　以上のような自由空間損失LOSに大地反射波損失REFを加算すると、以下の
　　ようなグラフ（一例）が得られます。




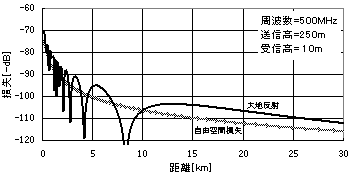
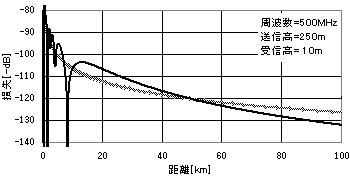
　　　この例では10km以下や8km付近に大きな落ち込みがありますが近距離なので
　　落ち込みによる影響は少ないといえます。とはいえ、このような落ち込みに
　　よって、特定の周波数(チャンネル)の受信強度に大きな違いが生じる場合が
　　あります。
　　　このような場合の対策方法はアンテナの高さを変えることです。高さを変
　　えると落ち込みを緩和出来たり、他の周波数に移動するからです。
　　　なお、この結果は完全平面の大地を想定していますが、実際には伝搬途中
　　の様々な障害物によって複雑な変化が積算されます。


周波数特性

　　　前節の大地反射の影響は周波数によっても異なります。下図は２つの異な
　　る周波数での伝搬の様子を示したグラフです。周波数を変化させると電波の
　　落ち込み部分が移動することが分かります。



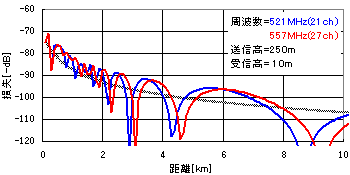
　　　ある地点で受信している場合は周波数によって電波の強度が異なる周波数
　　特性が生じます。下図は、送信所から３km離れた地点での周波数特性です。
　　横軸は周波数を示しており、539MHz(24ch)に大きな落ち込みが生じているの
　　が分かります。



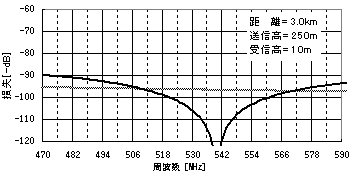
　　　以上までの例は大地に完全な平面の反射板が存在した場合の計算結果です。
　　現実の大地は凹凸があるため上図のとおりの特性が得られるわけではありま
　　せん。しかし、電波伝搬特性を検討するにあたって、最も大きな影響を及ぼ
　　す大地反射を考慮することで、特性の傾向を得ることが出来ます。そして、
　　大地がどのように影響するかを理解いただけたと思います。


見通し距離

　　出力が小さい場合は、遠くまで受信できませんが、出力が大きくなったり、
　　ワンセグ(１セグメント放送)では、受信器の受信感度が高いため、放送局か
　　ら、かなり離れた場所でも、受信できるようになります。
　　しかし、距離が離れれば離れるほど「地球が丸い」ことによる大地のカーブ
　　が問題になってきます。一般に、下記の距離を越えると、著しく損失が増加
　　するといわれています。

　　　　標準大気見通し距離 D_LOS ≒ 4.12*( sqrt(h1[m])+sqrt(h2[m]) )[km]

　　例えば、200mの高さから放送する場合、約70kmを超えると、大地の湾曲によっ
　　て、アンテナが見通せなくなります。


奥村-泰の伝播損失

　　フリスの自由空間損失は、障害物の無い伝播損失でした。また、最も大きな
　　障害物の大地の影響も説明しました。以上は、放送局のアンテナが見える場
　　合に、簡単に伝播損失を計算する公式でした。
　　しかし、都心部などでは、ビルに囲まれていて放送局のアンテナが、全く、
　　見えない場合があります。このような時に、使用するのが、奥村-泰(はた)の
　　伝播損失です。下式はエクセルシート等に貼り付けて使用ください。

　　・フリスの自由空間損失(LOS)

　　　　フリス[dB] ＝ 20*LOG(4*PI()*SQRT(DIST^2+(HT-HR)^2)/(300/FREQ))

　　・奥村-泰モデルの伝播損失(都市部)

　　　　奥村泰[dB] ＝ 69.55+26.16*LOG(FREQ)-13.82*LOG(HT)
　　　　　　　　　　　-((1.11*LOG(FREQ)-0.7)*HR-(1.56*LOG(FREQ)-0.8))
　　　　　　　　　　　+(44.9-6.55*LOG(HT))*LOG(DIST/1000)

　　・奥村-泰モデルの伝播損失(郊外)

　　　　郊外泰[dB] ＝ 奥村泰[dB]-2(log(FREQ/28))^2-5.4

　　・拡張泰モデルの伝播損失(都市部)

　　　　拡張泰[dB] ＝ 46.3+33.9*LOG(FREQ)-13.82*LOG(HT)
　　　　　　　　　　　-((1.11*LOG(FREQ)-0.7)*HR-(1.56*LOG(FREQ)-0.8))
　　　　　　　　　　　+(44.9-6.55*LOG(HT))*LOG(DIST/1000)+CM

　　　　　　　　　　　　　　　　　　　　　　　　FREQ : 周波数[MHz]
　　　　　　　　　　　　　　　　　　　　　　　　　HT : 送信局の高さ[m]
　　　　　　　　　　　　　　　　　　　　　　　　　HR : 受信アンテナ高[m]
　　　　　　　　　　　　　　　　　　　　　　　　DIST : 伝播距離[m]
　　　　　　　　　　　　　　　　　　　　　　　　　CM : 過密度(0〜3[dB])

　　このような障害物があるような伝播では、実態と計算が、あまり合いません。
　　しかも、これらは携帯電話の伝播損失の解析用ですので、放送では、送信局の
　　高さや伝播距離が携帯電話よりも大きい為、そのあたりも検証が必要です。
　　したがって、この式を使って、必要なアンテナ利得を求めるようなことは、
　　出来ませんが、数式を用いることで、電波伝搬に関する様々な検討が出来る
　　ようになります。

同軸ケーブルとの比較

　　冒頭に書いたとおり、電波は球面状に広がってゆくので、電波は薄まってゆ
　　きます。距離に対して２乗の減衰があります。このため送信アンテナから近
　　いところでは、少し離れるだけで大きな減衰があります。しかし、送信アン
　　テナから十分に離れた場所では、あまり減衰しなくなります。
　　下図の例では、0.5km以内では大きな急激に減衰していますが、2kmを離れる
　　と減衰が緩やかになっていることが分かります。



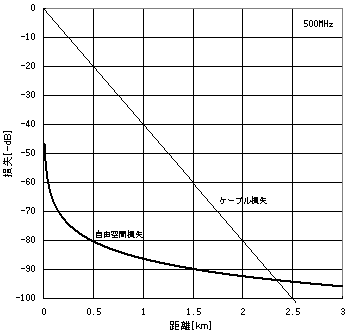
　　一方、同軸ケーブルの減衰は距離の変化に一定の直線となっています。また、
　　約2.3kmの部分で同軸ケーブルと自由空間減衰が交差しています。
　　つまり、この例では、2〜3kmを超えると同軸ケーブルよりも同じ電力の電波
　　の方が遠くまで伝播することが分かります。例えば、ケーブルテレビでは、
　　中継器による増幅が必要になりますので、地上デジタル放送の方がが省エネ
　　ルギーあることが分かります。反対に、2〜3kmに満たない距離ではケーブル
　　の方が効率が良いことも分かります。
　　例えばLANのような近距離での通信では、無線を使ったワイヤレスLANよりも、
　　有線LANの方が圧倒的に省エネルギーであることが分かります。

関連ページ

　　設計編 - 回線設計　　　　放送出力300W,LOS10kmでの設計例
　　基礎編 - 公式と定数　　　光速 透磁率 誘電率 VSWR 反射係数

地デジTopへ戻る